401. Prostakvaşinalı
Şarikin məktubu.
“Əzizim Fyodor
dayı!
Sən bu
deyingən qoca pişiyə qulaq asma. Ona nə sürpriz
hazırladığımdan hələ xəbərsizdir,
belə ki, siz indidən onun üçün proqram yaza
bilərsiniz. Mən onun üçün mötərizəli
kvagratların sayını 300 -ə, gündəlik
tapşırıqların sayını 20 –yə
qaldırdım və tapşırıqların mürəkkəbliyini
də artırdım.
İndi o, mötərizələrin
iç-içə düzgün yerləşmə
sayını da tapmalıdır. Bunun nə olduğunu mən
bir kitabdan oxumuşdum; onu poçtalyon Peçkin itirdi. Orada
yazılır:
“Tutaq ki, X
–düzgün qurulmuş mötərizəli ifadələrin
sayıdır. E -düzgün qurulmuş mötərizəli
ifadəsirin uzunluğu, E -də olan
mötərizələrin (bir-bir hamısı) sayı hesab
olunur. E çoxluğunda iç-içə
yerləşmə –D(E):
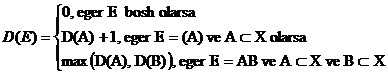
-kimi
hesablanır
Məsələn, ( )(( ))( ) ifadəsinin
uzunluğu 8, iç-içə
yerləməsi 2 –dir..
Hər
halda, pişiyin adam olmadığını nəzərə
alaraq elə məsələlər verirəm ki,
iç-içə yerləmə 1 –dən az və 200
–dən çox olmsın və mötərizəli
kvadrtların sayı isə ən az iki olsun. Bax indi qoy o, verilmiş
uzunluğa və iç-içə yerləşməyə
görə, bu cür düzgün mötərizəli
ifadələrin mümkn sayını tapsın görək.
Belə ki,
onun üçün yeni proqramı göndərməyə
tələs, yoxsa inəyi sağıb südü. ancaq
özm içirəm, hələ ki, Matroskin hesablama ilə
məğuldur. Düşüncəli Motroskinin şəklini
də əlavə edirəm.
Sənin
sadiq dostun və yoldaın –Şarik.
Giriş. Hər sətirdə
iki n və d ədədləri
yerləşir: n-verilən
mötərizəli kvadratların sayı, d – iç-içə yerləşmə
dərinliyi. Girişdə boş sətir olarsa o inkar edilir.
Çıxış. Hər test
üçün ayrıca sətirdə, n uzunluqlu və d dərinlikli
düzgün qurulmuş mötərizəli ifadələrin
mümkün sayı çixlarılır.
Girişə nümunə
6 2
300 150
Çıxışa nümunə
3
1
HƏLLİ
dinamik proqramlama
Alqoritmin
analizi
n uzunluqlu,
dərinliyi isə d –ni
aşmayan hər bir boş olmayan A mötərizəli
ifadəsini (X)Y kimi ifadə edə bilərik; burada X və Y
–boş olması da mmkün olan ifadələrdir.
Tutaq ki, (X) ifadəsinin uzunluğu k –dır. Onda X –in uzunluğu k -2, Y –in uzunluğu isə n-k olar. Təbiidir ki, 2 ≤ k ≤ n və demək k yalnız
dörd qiymət ala bilər. k
= 2 halında X boş ifadə, k
= n halında isə Y boş
ifadə olar. Onu da qeyd edək ki, A –nın dərinliyi d –dən çox
olmadığı üçün, X –in dərinliyi d – 1 –i, Y -in dərinliyi isə d.-ni aşmaz.
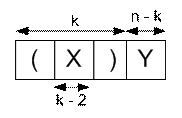
n uzunluqlu, dərinliy d –ni aşmayan,
düzgün qurulmuş mötərizəli ifadələrin
mümkün sayını f(n, d) ilə
işarə edək. O paman X ifaəsi f(k – 2, d – 1), və Y ifaəsi f(n
– k, d) variantla əldə edilə bilər. Hasil
qaydasını tətbiq etməklə təsdiq etmək olar
ki, qeyd olunmuş k üçün
(X)Y ifadəsi (k – 2, d – 1) * f(n – k, d)
variantda mövcud ola bilər. Beləliklə:
f(n, d) = 
Məsələdə
n uzunluqlu, dərinliyi d olan, düzgün qurulmuş
mötərizəli ifadələrin mümkün sayı
tələb olunduğu üçün cavab g(n, d)
= f(n, d) – f(n,
d – 1) olar.
Aşağıdakı
hallara isə ayrıca baxmaq lazımdır:
·
Əgər d > n / 2,
isə,
onda g(n,
d) = 0;
·
Əgər d = n / 2, isə,
onda yeganə ifadə
(((…))) alınar və g(n, n
/ 2) = 1;
·
Əgər d = 1, isə, onda yeganə ifadə ()()…()() alınar və g(n, 1) = 1;
Misal
f(2, 2) = 
= f(0, 1) * f(0, 2) = 1* 1 = 1. Əgər
uzunluğu 2 və dərinliyi 2 –ni aşmayan mötərizəli
ifadəni (X)Y kimi yazsaq,
onda f(0, 1) çoxluğu X –in, f(0, 2) isə Y –in
mümkün təsvir variantlarına uyğundur. Göstərilən
çoxluqlar vahidə bərabərdir, X və Y isə
boş ifadələrə uyğundur. Yəni, f(2, 2) –yə yeganə () ifadəsi uyğundur.
f(4, 2) = 
= f(0, 1) * f(2, 2) + f(2, 1) * f(0, 2) = 1 * 1 + 1 * 1 = 2.
Burada
birinci topllanan f(0, 1) * f(2, 2), ()() ifadəsinə uyğundur,
f(2, 1) * f(0, 2) isə, (()) ifadəsinə uyğundur.
f(6, 2) = 
= f(0, 1) * f(4, 2) + f(2, 1) * f(2, 2) + f(4, 1) * f(0, 2) =
1 * 2 + 1 * 1 + 1 * 1 = 4.
|
Toplanan |
Uyğun mötərizə ifadəsi |
|
f(0, 1) * f(4, 2) |
()()(), ()(()) |
|
f(2, 1) * f(2, 2) |
(())() |
|
f(4, 1) * f(0, 2) |
(()()) |
Uzunluğu
6, dərinliy isə 2 olan, düzgün
qurulmuş mötərizəli ifadələrin mümkün
sayı
g(6, 2) = f(6, 2) – f(6, 1) = 4 – 1
= 3 oar. Onlar: ()(()), (())() və (()()) ifadəəridir.
Alqoritmin
realizasiyası
f(n, d)
–nin qiymətlərini ff –uzun ədədlər massivində
saxlayaq.
BigInteger ff[301][151];
f funksiyası f(n, d) nin
qiymətini hesabayır. n < 0 və ya d < 0 kimi xüsusi hallara ayrıca baxılır (bu hallarda funksiya 0
cavabı verir). Əgər n = 0 isə, onda f(0, d) –ni
istəniən d üçün
1 -ə bərabər sayırıq. (bu hal, ya X, ya da Y –in boş omasına uyğundur).
BigInteger f(long
long n, long long d)
{
long long
k;
BigInteger &s = ff[n][d];
if ((n < 0) || (d < 0)) return 0;
if (!n) return
ff[n][d] = BigInteger(1);
if (ff[n][d] >= 0) return ff[n][d];
for(s = 0, k = 2; k <= n; k += 2)
s = s + f(k - 2,d - 1) * f(n - k,d);
return s;
}
Proqramın
əsas hissəsi. Əvvəlcə xüsusi hallara baxılır.
memset(ff,-1,sizeof(ff));
while(scanf("%lld %lld",&n,&d)
== 2)
{
if (d > n / 2) res = BigInteger(0); else
if ((d == n / 2) || (d == 1)) res =
BigInteger(1); else
res = f(n,d) - f(n,d-1);
res.print();printf("\n");
}
Java
üzrə realizə
import java.util.*;
import java.math.*;
public class
{
static
BigInteger dp[][];
static
BigInteger f(int n, int
d)
{
BigInteger s = BigInteger.ZERO;
if ((n <
0) || (d < 0)) return BigInteger.ZERO;
if (n == 0)
return dp[n][d] = BigInteger.ONE;
if
(dp[n][d].compareTo(BigInteger.ZERO) >= 0) return
dp[n][d];
for(int k = 2; k <= n; k += 2)
s = s.add(f(k - 2,d - 1).multiply(f(n -
k,d)));
return
dp[n][d] = s;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
while(con.hasNextInt())
{
int n =
con.nextInt();
int d =
con.nextInt();
dp = new
BigInteger[n+1][d+1];
for(int i = 0; i <= n; i++)
for(int j = 0; j <= d; j++)
dp[i][j] = new
BigInteger("-1");
BigInteger res = new
BigInteger("0");
if (d
> n / 2) res = BigInteger.ZERO; else
if ((d ==
n / 2) || (d == 1)) res = BigInteger.ONE; else
res = f(n,d).subtract(f(n,d-1));
System.out.println(res);
}
con.close();
}
}